Обратите внимание на то, что первые два условия в левой части правила являются истинными независимо от значения ζ. Поэтому их можно удалить из данного правила, что приводит к получению такого соотношения: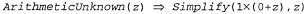

Рис. 19.5. Деревья доказательства для рассматриваемой задачи упрощения. Первое дерево демонстрирует доказательство для первоначального экземпляра задачи, на основании которого можно вывести следующее:

Второе дерево демонстрирует доказательство для экземпляра задачи, в котором все константы заменены переменными, что позволяет вывести целый ряд других правил

Вообще говоря, из окончательного правила можно удалять такие условия, которые не налагают ограничений на переменные в правой части правила, поскольку при этом результирующее правило остается истинным и становится более эффективным. Обратите внимание на то, что условие ArithmeticUnknown(z) удалять нельзя, поскольку не все возможные значения z являются арифметическими неизвестными. Для значений, отличных от арифметических неизвестных, могут потребоваться другие формы упрощения; например, если переменная z равна 2x3, то правильным упрощением выражения 1х (0+ (2x3) ) должно быть б, а не 2x3.

Подводя итог, можно отметить, что основной процесс обучения на основе объяснения действует, как описано ниже.

1.    Используя рассматриваемый пример, составить доказательство того, что целевой предикат является применимым к данному примеру, с использованием доступных фоновых знаний.

2.    Одновременно с этим сформировать обобщенное дерево доказательства для цели, описанной с помощью переменных, в котором используются такие же этапы логического вывода, как и в первоначальном дереве доказательства.

3.    Сформулировать новое правило, левая часть которого состоит из листовых узлов дерева доказательства, а правая часть представляет собой цель, описанную с помощью переменных (после применения соответствующих связываний из обобщенного доказательства).

4.    Удалить все условия, которые являются истинными независимо от значений переменных в цели.